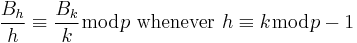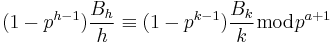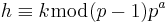Kummer's congruence
In mathematics, Kummer's congruences are some congruences involving Bernoulli numbers, found by Ernst Eduard Kummer (1851).
Kubota & Leopoldt (1964) used Kummer's congruences to define the p-adic zeta function.
Statement
The simplest form of Kummer's congruence states that
where p is a prime, h and k are positive even integers not divisible by p−1, and the numbers Bh are Bernoulli numbers.
More generally if h and k are positive even integers not divisible by p − 1, then
whenever
The two sides of the Kummer congruence are essentially values of the p-adic zeta function, and the Kummer congruences imply that the p-adic zeta function for negative integers is continuously, so can be extended by continuity to all p-adic integers.
See also
- Von Staudt–Clausen theorem, another congruence involving Bernoulli numbers
References
- Koblitz, Neal (1984), p-adic Numbers, p-adic Analysis, and Zeta-Functions, Graduate Texts in Mathematics, vol. 58, Berlin, New York: Springer-Verlag, ISBN 978-0-387-96017-3, MR754003
- Kubota, Tomio; Leopoldt, Heinrich-Wolfgang (1964), "Eine p-adische Theorie der Zetawerte. I. Einführung der p-adischen Dirichletschen L-Funktionen", Journal für die reine und angewandte Mathematik 214/215: 328–339, ISSN 0075-4102, MR0163900, http://gdz.sub.uni-goettingen.de/dms/resolveppn/?GDZPPN002180626
- Kummer, Ernst Eduard (1851), "Über eine allgemeine Eigenschaft der rationalen Entwicklungscoëfficienten einer bestimmten Gattung analytischer Functionen", Journal für Reine und Angewandte Mathematik 41: 368–372, ISSN 0075-4102, JFM 041.1136cj, http://resolver.sub.uni-goettingen.de/purl?GDZPPN002147319